波函数基础
平面单色波函数:
\[ \psi(r,t) = \phi e^{i(k \cdot r-\omega t)} \]
其中\(k=2\pi/\lambda\)为波数,\(\omega=2\pi f\)为角频率。其振幅\(\phi\)不随时间变化,为定态波函数(并不意味着波函数不随时间变化)。
波函数来自于下面的二阶偏微分方程,平面单色波是其一个特解:
\[ \frac{\omega^2}{k^2} \nabla^2 \psi = \frac{\partial^2 \psi}{\partial t^2} \]
对于平面波,等相位面\(\phi = k \cdot r-\omega t = const\),将坐标对时间求导可得相速度:
\[ \frac{dr}{dt} = \frac{\omega}{k} \]
波包
实际情况中波动的振幅只在空间的有限区域内不为零,所以形象地称之为波包。
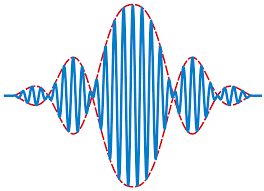
蓝色实线为波包,红色虚线为包络线。
通常波包可由不同波数\(k\)的波叠加而成,可写为:
\[ \psi(r, t) = \sum_k \phi(k) e^{i(k \cdot r-\omega(k)t)} \]
或将波数\(k\)考虑为连续变化,写为积分形式(Fourier逆变换):
\[ \psi(r, t) = \int \phi(k)e^{i(k \cdot r - \omega(k)t)} dk \]
其中\(\phi(k)\)为每一个单色波的振幅,角频率\(\omega(k)\)与波数\(k\)的函数关系称为波的色散关系。
考虑在\((r_c, t)\)处波包的振幅达到最大,那么波包经过传播,在\((r_c+\Delta x, t+\Delta t)\)时再现\((r_c, t)\)处的各个频率的相位,所以相位对于频率的导数应为0:
\[ \frac{d \phi}{d k} = r_c - \frac{d \omega}{d k}t = 0 \]
再对时间求导可得群速度:\(\frac{d r_c}{d t} = \frac{d \omega}{d k}\)。
波函数的Fourier变换
所以我们可以考虑对处于\(t=0\)时刻的波包\(\psi(r, 0)\)乘以某一个单色波相因子的共轭:\(e^{-ik \cdot r}\),根据三角函数积分的正交性,我们就可以得到该单色波的振幅\(\phi(k)\):
\[ \phi(k) = \frac{1}{2 \pi} \int \psi(r, 0)e^{-ik \cdot r} dr \]
\(\frac{1}{2\pi}\)来自于对三角函数周期区间积分所得结果。另外如果将\(\psi(r, t)\)的表达式代入,根据\(\delta\)函数的性质,可以得到相同结果:
\[ \begin{aligned} \frac{1}{2 \pi} \int \psi(r, 0) e^{-i k \cdot r} dr &= \frac{1}{2 \pi} \int e^{-i k \cdot r} dr \int \phi(k') e^{i k' \cdot r} dk' \\ &= \int \phi(k') dk' \int \frac{1}{2 \pi} e^{i(k'-k) \cdot r} dr \\ &= \int \phi(k') \delta(k'-k) dk' \\ &= \phi(k) \end{aligned} \]