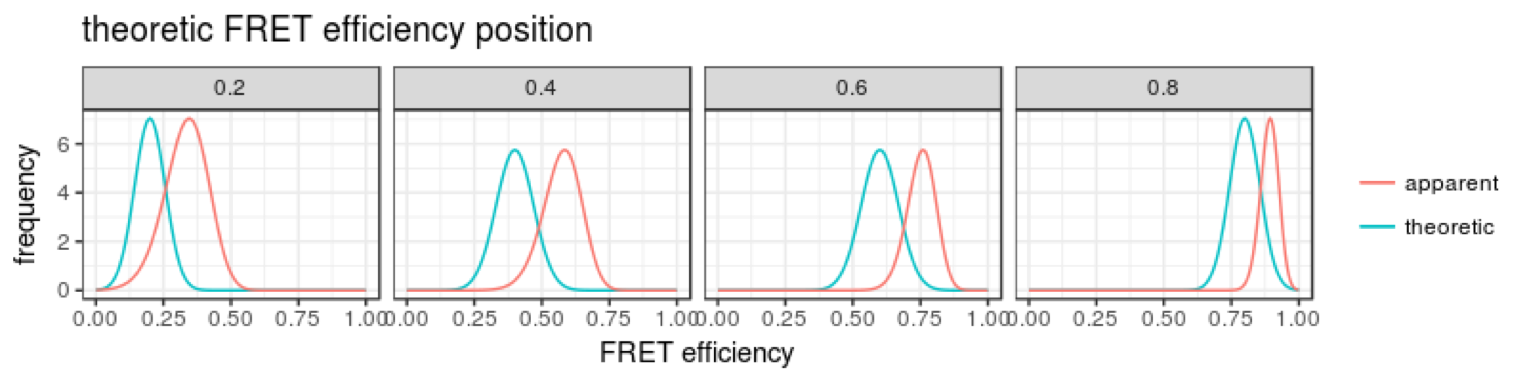
荧光共振能量转移(Förster resonance energy transfer, FRET)是生化实验中的常见手段,一般用于检测生物大分子是否有相互作用、共定位或构象变化。
单分子FRET(single-molecule FRET, smFRET)将单分子超高时空分辨率的优势和FRET对距离变化的敏感性结合起来,是研究蛋白分子构象变化的有力武器。然而由于噪音、荧光染料自身性质和仪器检测效率等原因,我们只能得到表观的测量值,所以需要对其进行校正。
背景噪音
背景噪音在时间分辨率\(dt\)的情形下,光子数的分布服从Poisson分布,\(I_b \sim P(\lambda)\),其中\(\lambda = r \cdot dt\),\(r\)为背景噪音的光子产生速率。首先需要对采集到的原始信号\(I_D\)和\(I_A\)扣除背景,对于背景噪音的拟合有三种办法。
平均值法
将收集得到的单分子荧光trace直接求平均。由于一段荧光时间序列中的大部分都是噪音,所以直接求平均值(或给定一个阈值上限,排除掉由荧光分子产生的有效信号),就可近似地得到平均噪音水平。
对噪音的光子数分布进行拟合
在一段单分子荧光trace中,噪音会一直存在,而荧光分子只有经过聚焦体积时才会发出荧光,所以对于一段合适的荧光trace,大部分信号应该都是噪音,所以其光子数分布应该为一开始一个很高的poisson分布,再叠加上很小一部分的指数分布,该指数分布是由于荧光染料分子进入聚焦体积发光而产生的,对于噪音的poisson分布影响很小。所以我们可以对光子数分布的前面部分(例如前80%)进行Poisson拟合,从而得到平均噪音水平。
对噪音的光子寿命进行拟合
因为\(I_b \sim P(\lambda)\),所以噪音光子的抵达时间的间隔\(\tau_b \sim E(\lambda)\),可以通过时间相关单光子计数卡(time-correlated single photon counting, TCSPC)根据光子的间隔时间来区分背景噪音和有效信号。
因为Poisson分布和Exponential分布密切相关,所以本质上和对光子数分布进行拟合是一样的。
漏光
Donor染料的发射光谱通常会有一部分和Acceptor通道的滤光片透光波段重叠,使得Acceptor通道可以检测到部分来自Donor的光子。这部分信号强度和Donor在Donor通道的信号强度呈正比,通常可以采用Donor-only的样品,检测其在两个通道的信号强度,然后做比得到Donor在Acceptor通道的漏光系数 \(\alpha\)。
\[ \alpha = \frac{I_A}{I_D} \]
也可以在测量双标样品的single-molecule FRET后,通过零峰的位置进行校正。因为漏光,校正前零峰不在FRET效率=0的位置,然而既然都叫零峰,其理论值=0,所以根据下式:
\[ \alpha = (E^{-1} -1)^{-1} \]
量子产率与接收效率
在FRET过程中,不考虑漏光和直接激发的情况下,Donor和Acceptor发光强度为:
\[ \begin{aligned} I_D &= I_0 \sigma_D Q_D \eta_D (1-E) \\ I_A &= I_0 \sigma_D Q_A \eta_A E \\ \end{aligned} \]
其中\(I_0\)为激发光光强,\(\sigma_D\)为Donor荧光分子的吸收截面,\(Q_D\)和\(Q_A\)为对应的量子产率,\(\eta_D\)和 \(\eta_A\)为对应通道的接收效率,\(E\)为理论FRET效率。对上式微分可得:
\[ \begin{aligned} dI_D &= I_0 \sigma_D Q_D \eta_D \cdot d(-E) \\ dI_A &= I_0 \sigma_D Q_A \eta_A \cdot dE \\ \end{aligned} \]
我们可以设想一个Acceptor先于Donor猝灭的过程,这样Donor通道的信号强度会增加\(\Delta I_D\),Acceptor通道的信号强度会降低\(\Delta I_A\),FRET效率会从\(E\)降到0,通过TIRF可以将Acceptor猝灭的过程挑出来,并测到\(\Delta I_D\)和 \(\Delta I_A\),将上两式相除,就可以得到:
\[ \gamma_T = \frac{Q_A \eta_A}{Q_D \eta_D} = \frac{\Delta I_A}{\Delta I_D} \]
这样就得到了TIRF的校正系数\(\gamma_T\)。
对于Confocal显微镜,需要用一个双标的标准样品,在TIRF上测出一个理论值,再在Confocal显微镜上测FRET效率,根据理论值来反推出校正系数\(\gamma_c\)。
\[ \gamma_c = \frac{E^{-1}-1}{E_{app}^{-1}-1}\]
其中\(E\)为通过TIRF测得的标准样的FRET效率理论值,\(E_{app}\)为标准样品在Confocal上测得的扣除了背景和漏光的表观FRET效率值。在得到了校正系数\(\gamma_c\)后,Confocal的校正公式为:
\[ E = (1+\gamma_c \frac{I_D}{I_A})^{-1} \]
其中\(I_D\)与\(I_A\)是校正了背景和漏光后的信号。
直接激发
直接激发项的校正需要用到ALEX (Alternating-Laser Excitation)激光光源,这在国内配备得较少,不过随着发展,应该会逐渐成为Confocal单分子测量的标配。简单讲,对于Acceptor-only的样品,有以下关系:
\[ \begin{aligned} I_A^{Dex} &= I^{Dex} \sigma^{Dex}_{A} Q_A \eta_A \\ I_A^{Aex} &= I^{Aex} \sigma^{Aex}_{A} Q_A \eta_A \\ \end{aligned} \]
其中上标的\(Dex\)和\(Aex\)代表了采用Donor激发光还是Acceptor激发光,将两式相除就可得到直接激发的校正系数\(d\):
\[ d = \frac {I^{Dex} \sigma_A^{Dex}}{I^{Aex} \sigma_A^{Aex}} \]
于是直接激发项可以表示为:
\[ I_A^{Dex} = d \cdot I_A^{Aex} \]
在ALEX实验中对Acceptor通道信号减掉直接激发项即可。
##Jacobian行列式
Jacobian行列式常用于积分换元:
\[ J = \left| \begin{matrix} \frac{\partial x_1}{\partial u_1} &\cdots &\frac{\partial x_1}{\partial u_k} \\ \vdots & \ddots & \vdots \\ \frac{\partial x_k}{\partial u_1} &\cdots &\frac{\partial x_k}{\partial u_k} \\ \end{matrix} \right| \]
通常可写为\(\frac{\partial (x, y)}{\partial (u, v)}\)。Jacobi行列式具有下列重要性质:
\(\left( \frac{\partial u}{\partial x} \right)_y = \frac{\partial (u, y)}{\partial (x, y)}\)
\(\frac{\partial (u, v)}{\partial (x, y)} = -\frac{\partial (v, u)}{\partial (x, y)} = \frac{\partial (-v, u)}{\partial (x, y)}\)
设\(u, v, r, s\)都是独立变量\(x, y\)的函数,则:\(\frac{\partial (u, v)}{\partial (x,y)} = \frac{\partial (u, v)}{\partial(r, s)}\frac{\partial (r, s)}{\partial (x, y)}\)
\(\frac{\partial (u, v)}{\partial (x,y)} = 1/\frac{\partial (x,y)}{\partial (u, v)}\)
对于一维情况: \[ \begin{aligned} x &= x(u) \\ \int f(x)dx &= \int f(x(u)) \cdot \frac{dx}{du} \cdot du \\ \end{aligned} \]
在FRET分布的校正中,理论FRET效率的概率密度函数应该服从高斯分布\(N(\mu, \sigma)\),而校正前的FRET效率的概率密度函数暂时未知,但是有如下关系:
\[ f(E_{app}) = F(E)\cdot \frac{dE}{dE_{app}} \]
其中\(F(E) = Ae^{\frac{-(E-\mu)^2}{2\sigma^2}}\)为理论FRET分布的概率密度函数,根据FRET的校正公式:
\[ E^{-1}-1 = \gamma_c \cdot (E^{-1}_{app}-1) \]
可得到:
\[ \frac{dE}{dE_{app}} = \gamma_c \cdot \frac{E^2}{E_{app}^2} \]
代入上式即可得到表观FRET分布的概率密度函数\(f(E_{app})\)。
当校正系数\(\gamma\)取不同值时,理论FRET效率与表观FRET效率呈非线性关系:
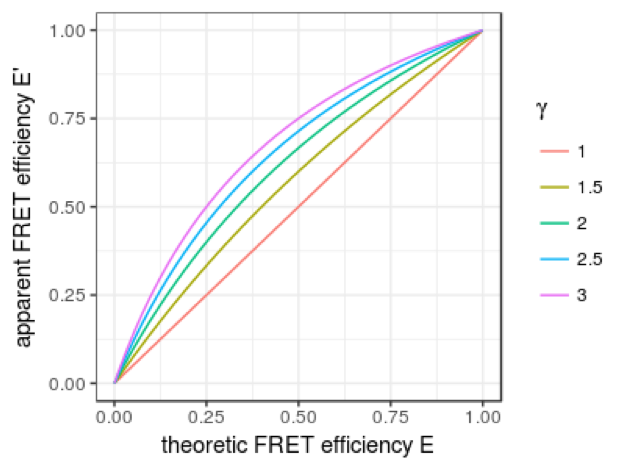
校正前的FRET分布呈现偏态: